傳送門:
PolandBall and Polygon
題意:
有N個點的凸多邊形且對角線任三條不交於同點,每點依順時針方向編號,現在從任一點開始往後數K個連一條對角線,再由此點繼續出發重複上個步驟共畫N次,每畫一條對角線就輸出目前多邊形被切成幾個區塊。
\( 5<=N<=10^{6} \),\( 2<=K<=N-2 \),\( GCD(N,K)=1 \)
思路:
這題看上去還挺難的,嚇得我當時直接往後面一題看,不過又被嚇回來就是了XD
首先把圖畫出來觀察一下
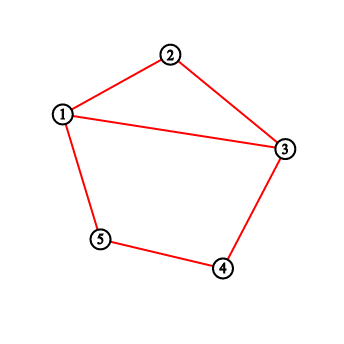
發現以下幾點:
- 起始時共有1個區塊(ans=1)
- 從A點連到B點的線段與從A+1、A+2、⋯⋯、B−1連到不包含A、A+1、⋯⋯、B相交
接著我們再畫幾條線來發現直線與M條線相交時,將平面切出M+1個新的區塊,現在,我們剩下一個問題。
從區間(A,B)連出去的線到底有多少?
因為每點都是固定與往後數第K點連線,所以區間(A,B)內的點一定只往區間外連,畢竟內部自己連就<K了,所以我們只需要知道區間(A,B)連幾條線了,之後每次連線時就把A點與B點的連線數量+1。
至此,問題已被剝去層層外衣(咦?),我們需要做的是提供 區間詢問、單點更新,有一大把的方法來對付這種問題,這邊我是用BIT(Binary Indexed Tree/Fenwick Tree)來喇過的,之後,我們來繼續分析如何做詢問以及更新。
因為GCD(N,K)=1,得知在前N次必定不會畫出起點終點相同的線段,導致畫了線卻沒有切出新區塊,原因類似取 mod N,互質所以前N次不會碰撞。
接著,往後數第K個點等價於往後數第N−K個點,挑小的做吧!
最後,把區間以B有無大於N來分類,再仔細思考區間該如何下即可結束這回合,以下講解code。
code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
//hi~ :)
#include <bits/stdc++.h>
#define fastio ios::sync_with_stdio(false);cin.tie(0)
using namespace std;
typedef long long ll;
ll N,M,a,b,c;
ll bit[3000000];
inline int lowbit(int x) {
return x&(-x);
}
void update(int pos, int val){
for(int i=pos; i<=N;i+=lowbit(i))
bit[i] += val;
}
ll sum(int k){
ll ans=0;
for(int i=k;i>0;i-=lowbit(i))
ans+=bit[i];
return ans;
}
ll query(int l, int r){
ll ans=0;
if(r<l){ // 分成有無>N處理
ans += sum(N);
ans -= query(r-1, l+1);
}
else{
ans += sum(r-1);
ans -= sum(l);
}
return ans;
}
int main(){
fastio;
int ncase=1;
while(ncase--){
cin>>N>>M;
if(2*M > N) M=N-M; // 挑小的做省麻煩
memset(bit, 0, sizeof(bit));
ll ans=1;
for(int i=0,l=1,r;i<N;i++){
r = ((l+M>N)?(l+M-N):(l+M)); // >N記得從頭開始
ans += (query(l, r)+1); // 區間詢問來更新答案
update(l,1); // 維護BIT
update(r, 1);
l=r; // 從這個點繼續開始
cout<<ans;
if(i+1<N)cout<<" ";
}
cout<<endl;
}
}