傳送門:
Tree Folding
題意:
給一棵無根樹,每個節點下長度相同的鏈可以合併,最後把樹併成一條最短的鏈,求鏈長度。
若無法合併成一條鏈,輸出-1。
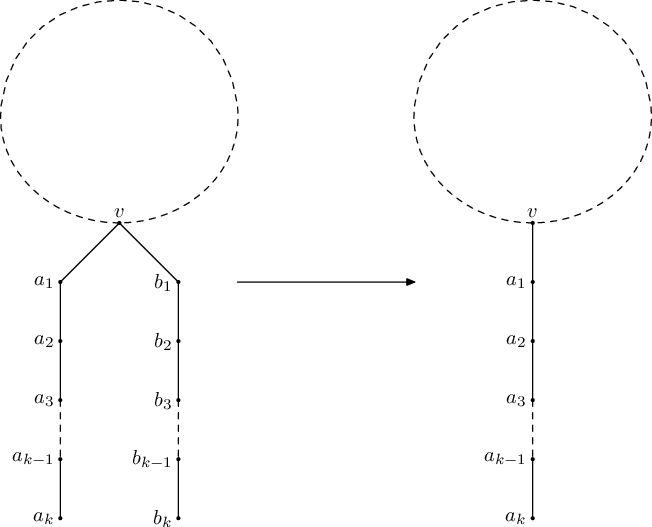
思路:
這題看第一眼覺得很麻煩也來不及刻出來,賽後我在 comments 區發現一個 keypoint。
把樹直徑的中點當root
如此一來,麻煩的合併操作在子樹內進行,此題分成兩個小問題來解決:
找出樹直徑的中點
合併操作
1. 找出樹直徑的中點
我使用比較簡單的3次dfs方式,第一次dfs隨便挑一個點找最深處,第二次dfs從上次的最深處開始邊走邊給各點上距離標記,一樣找最深處,第三次dfs再從上次的最深處開始,找到直徑上的中點。
兩次dfs找的最深處即是樹直徑的兩端點,維護距離標記是為了找出距離兩端點等長的地方(中點)。
對應下方code,第一二次 dfs 是 dfs1,第三次則是 dfs2
2. 合併相同長度的鏈
我的做法是一邊爬樹一邊維護目前的鏈的長度,每個節點用map記下子樹鏈長的種類,回傳合併後的長度或不可合併(-1)
對應下方code的merge
最後從直徑中點來合併各個子樹,把鏈長搖一搖AC
code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
//hi~ :)
#include <bits/stdc++.h>
#define X first
#define Y second
using namespace std;
typedef pair<int,int> pii;
typedef vector<int> vi;
int N,h[200005],a,b;
vi G[200005];
map<int, int> child[200005];
void init(){
scanf("%d", &N);
for(int i=1;i<N;i++){
scanf("%d %d", &a, &b);
--a,--b;
G[a].PB(b);
G[b].PB(a);
}
}
int dfs1(int v, int pa){
int res = v, tmp;
for(int i : G[v])if(i!=pa){
h[i] = h[v]+1;
tmp = dfs1(i, v);
if(h[tmp] > h[res])
res = tmp;
}
return res;
}
int dfs2(int v, int pa, int dep){
if(abs(dep-h[v])<2)
return v;
for(int i:G[v]) if(i!=pa){
int res = dfs2(i, v, dep+1);
if(res != -1) return res;
}
return -1;
}
int merge(int v, int pa){
int res;
for(int i:G[v])if(i!=pa){
res = merge(i, v);
if( res == -1) return res;
child[v][res] ++;
}
if(child[v].size() > 1) return -1;
auto i = child[v].begin(); // 判斷有無子樹
return ( (i == child[v].end()) ? (1) : (1+(*i).X) );
}
void sol(){
int p1, p2, mp, tmp, res=0;
p1 = dfs1(0, 0);
h[p1] = 0;
p2 = dfs1(p1, p1);
mp = dfs2(p2, p2, 0);
for(int i : G[mp]){ // merge all subtree of mid point
tmp = merge(i, mp);
if(tmp == -1){
puts("-1");
return;
}
child[mp][tmp] ++;
}
if(child[mp].size() > 2){
puts("-1");
return;
}
for(pii i : child[mp])
res += i.X;
while(~res & 1) res>>=1;
printf("%d\n", res);
return ;
}
int main(){
init();
sol();
}